Random Values

The Methodical Application of Chance

We use the word random to mean an hodgepodge of related ideas. Depending on context, we might mean unplanned, unexpected, unpatterned, uncontrolled, unbiased, or unpredictable. Each of these are important characteristics in many procedural systems. Randomness is a staple of procedural generation systems, and careful control of randomness is important to balancing chance and control.

As an example consider the 18th-century composition Instructions for the composition of as many waltzes as one desires with two dice, without understanding anything about music or composition, which may have been written by Mozart. Rather than a fixed score, Instructions is a collection of pre-composed musical phrases a set of rules for using dice to select and order the phrases to create a unique composition. By leaving some aspects to chance while controlling others, the system ensures that each variation makes musical sense.

Using random values in your procedural system doesn’t mean your results must be haphazard, uncontrolled, or unorganized. While individual random values are unpredictable, with planning you can use these values to create a coherent cumulative effect.

Vera Molnar

(Dés) Ordres, 1974

Vera Molnar is one of the best-known pioneers of computer art. In this series, Vera presents grids of randomly shifted concentric squares.

(Dés) OrdresDigital Art Museumveramolnar.comArtist Site

LIA

Four Seasons: Spring, 2019

In this work, LIA interprets springtime into blossom-like, abstract forms. The elements are randomly generated and never repeat.

Four Seasons: SpringProject Pageliaworks.comArtist Site

Jean Arp

Collage with Squares Arranged According to the Laws of Chance, 1917

Jean Arp created this collage by allowing gravity control where the scraps of paper should land.

Collage with Squares...MoMA

Rafael Lozano-Hemmer

Method Random, 2014

Rafael explored randomness in these chromogenic prints by using a random number generator to assign what color each pixel should be.

Method RandomCase Studylozano-hemmer.comArtist Site

Amy Goodchild

Geometric Constellations, 2020

Amy created these constellation-like forms, each unique because of its random placement of nodes and connections.

amygoodchild.comArtist Site

Marcel Duchamp

3 Standard Stoppages, 1913

Marcel Duchamp dropped three horizontal threads onto three stretched canvases, where they were then adhered, in order to preserve the random curves they assumed upon landing. The canvases were cut along those curves, creating a template for new units of measure that retain the meter’s length but undermine its rational basis.

3 Standard StoppagesMoMA

Micheal Toy and Glenn Wichman

Rogue, 1980

Rogue was a genre-inspiring fantasy game with procedurally generated dungeons.

RogueWikipediaRoguelikeWikipedia

Random Numbers and Dice

Most programming languages provide a function for generating random numbers. Usually, the values provided are evenly distributed over the range 0 to 1. Mapping these values to your desired ranges and biasing their distribution are fundamental skills.

Generating Random Numbers

Plain JavaScript provides Math.random() to generate a random number.

The Math.random() function returns a floating-point, pseudo-random number in the range [0, 1); that is, from 0 (inclusive) up to but not including 1 (exclusive), which you can then scale to your desired range. The implementation selects the initial seed to the random number generation algorithm; it cannot be chosen or reset by the user.

MDN Documentation

Specifying a Range

Math.random() always gives you a value between 0 and 1. If you want a different range, you can scale and offset the value yourself:

Math.random() * range + start;

// e.g. even distribution between [10 and 15)
Math.random() * 5 + 10;

Random Integers

The Math.random() function returns floating point values, but sometimes you just want integers. The Math.floor() function will round a number down.

// roll a standard die
Math.floor(Math.random() * 6) + 1;

Be careful when generating integers: it is easy to get results that are slightly off. Math.floor() rounds down to the nearest integer, so you need to have values that go above the highest integer you want returned.

Using Math.round() instead of Math.floor() can lead to unevenly distributed results. In the example below, 1 will get picked half as often as it should, and 7 will sometimes get picked though it should not.

// roll a standard die
// this won't quite work. why?
Math.floor(Math.random() * 7);

// this also doesn't quite work. why?
Math.round(Math.random() * 6) + 1;

Creating a Utility Function

The expressions above are already getting complicated enough to negatively impact readability. Look at the code below. How quickly can you determine the minimum and maximum value that might be assigned to strength? How confident are you?

let strength = Math.floor(Math.random() * 6) + 10;

One way to improve the readability of this code is to create and use a utility function.

let strength = randomInt(10, 15);

// return a random integer between min and max (inclusive)
function randomInt(min, max) {
  return Math.floor(Math.random() * (max - min + 1)) + min;
}

The randomInt() function above returns a random integer between min and max, inclusively. This is different from random(), which returns values exclusive of max. I decided to design the function to work this way because I felt it was more natural to be inclusive for whole numbers, as in the phrase “pick a number between 1 and 10” which is generally understood to be inclusive.

p5 random()

Processing provides the random() function for generating random numbers. If called without any parameters, random() works very much like Math.random() producing numbers in the range [0, 1).

console.log("random()"); // random()
console.log(random()); // 0.45...
console.log(random()); // 0.12...
console.log(random()); // 0.37...

p5’s random() function accepts optional parameters to control the range of the number, so you don’t have to do it yourself.

console.log("random(10)"); // random(10) -> range [0, 10)
console.log(random(10)); // 4.89...
console.log(random(10)); // 1.20...
console.log(random(10)); // 6.99...

console.log("random(20, 30)"); // random(20, 30) -> range [20, 30)
console.log(random(20, 30)); // 21.96...
console.log(random(20, 30)); // 20.56...
console.log(random(20, 30)); // 22.36...

p5 provides floor() which you can use to generate random integers.

// roll a standard die
floor(random(0, 6)) + 1;
// or
floor(random(1, 7));

// this won't quite work. why?
floor(random(1, 6));

Biasing the Distribution

The random() function produces results that are approximately uniformly distributed: all values are equally likely.

Sometimes, uniform distribution is exactly what you want. If you are randomly choosing who gets to go first in a game, all the players should have an equal chance.

Other times, uniform distribution isn’t what you really want. If you are drawing a forest scene, you might want mostly short trees, some middle-height trees, and only a few very tall trees.

With some math, you can reshape the values returned by random() to just about any distribution you can think of. Often, you won’t need anything very complicated. Just biasing the results toward the low end, high end, or middle is often enough to achieve appealing effects. The calculations for creating these types of distributions are easy enough that you’ll often see them used as mechanics in tabletop role-playing games without the need for a computer.

Uniform Distribution

Generally, random functions provide uniform distribution. You don’t need to do anything if that is what you want.

randomInt(1, 10);

Try 1d10 on anydice.com

Low Bias

Taking the lowest of two or more random numbers will bias the result toward the low end. The p5 min() or JavaScript Math.min() function returns the lowest value among the provided arguments.

min(randomInt(10), randomInt(10));

The more random numbers you compare, the stronger the bias. Both the p5 and JavaScript min() functions can accept as many arguments as you want.

min(randomInt(10), randomInt(10), randomInt(10), randomInt(10));

Try [lowest 1 of 5d10] on anydice.com

High Bias

Taking the highest of two or more random numbers will bias the result toward the high end. The p5 max() or JavaScript Math.max() function returns the highest value among the provided arguments. Like the low bias example, the more random numbers you compare, the stronger the bias.

max(randomInt(10), randomInt(10));

Try [highest 1 of 2d10] on anydice.com

Middle Bias

Averaging two or more random numbers will bias the result toward the middle.

(randomInt(1, 10) + randomInt(1, 10)) / 2;

Try 2d10 / 2 on anydice.com

Normal Distribution

If you generate three or more random numbers and average them, the results approach a normal distribution. Normal distribution, or Gaussian distribution, is the “bell curve” distribution which is often found in natural systems. It occurs when multiple independent chances combine. For example, many factors contribute to how fast a tree may grow, so we might expect tree heights—in one area, for trees of the same age—to follow a normal distribution.

(random(1, 11) + random(1, 11) + random(1, 11)) / 3;

Try 3d10 on anydice.com

Random Orders and Decks

The random() function works a lot like rolling a die. When you roll a die, you get random values. Each value should be equally probable and each roll should be independent. If you roll the die multiple times, you might get the same value more than once, and it might take a long time to get a particular value.

These types of effects can be counter-intuitive and sometimes aesthetically undesirable.

If you roll a normal die six times, it is unlikely—about a 1.5% chance—that you’ll get all six values without repeats. You have a pretty good chance—about 33%–of not rolling any 1s. You can be pretty sure—98.5% sure—that at least one number won’t have appeared after six rolls.

A deck of cards works differently. When you pull cards from a deck, you don’t get random values. You get values in a random order. You avoid duplicates, and you know you will have toured all the values when you reach the end of the deck.

Modeling a Deck with an Array

p5 provides the shuffle() function to randomly reorder the elements in an array. By using shuffle() we can simulate shuffling a deck, pulling values from it, and reshuffling when we run out.

// create an array to hold the possible values
var values = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];

// create a variable to hold the current position in the deck
var position = 0;

function setup() {
  // shuffle the deck first
  values = shuffle(values);

  // pull as many values as we need
  for (let i = 0; i < 50; i++) {
    console.log(valueFromDeck());
  }
}

function valueFromDeck() {
  // find the value at the current position in the deck
  var v = values[position];

  // change the position for next time
  position++;

  // if that was the last value, shuffle and start over from the top
  if (position == values.length) {
    values = shuffle(values);
    position = 0;
  }

  // return the value
  return v;
}

Dice Visualizer

This visualizer simulates rolling a 10-sided die. It chooses a random value every time you click and plots a histogram of the results. The expected distribution is uniform. In practice, if you roll a few dozen times, you are likely to see some numbers come up much more often than other numbers. After hundreds or thousands of rolls, the results should even out.

Deck Visualizer

This visualizer simulates choosing numbers from a deck with 10 cards. It pulls the top card every time you click. When the deck runs out, it is shuffled. Using a deck ensures that the numbers come up very evenly, though the order is random.

Random Choices

If you want your code to make a decision at random, you can combine random() with a conditional—if—statement.

// do something only half the time
if (random() < 0.5) {
  console.log("Optional Thing");
}

// do something only 10% of the time
if (random() < 0.1) {
  console.log("Rare Thing");
}

// another way to do something only 10% of the time
if (random(100) < 10) {
  console.log("Rare Thing");
}

With else you can pick between two options and guarantee that one or the other will happen.

// do one thing, or the other. even odds.
if (random() < 0.5) {
  console.log("Option A");
} else {
  console.log("Option B");
}

With else if you can pick between multiple optional things to do.

var r = random(100);

if (r < 20) {
  // r is < 20
  console.log("Rare Thing 1 (20%)");
} else if (r < 40) {
  // r is >= 20 and < 40
  console.log("Rare Thing 2 (20%)");
} else {
  // r is >= 40
  console.log("Common Thing (60%)");
}

A common mistake when following this pattern is calling random multiple times. If you are making one choice between several options, you only want to call random() once.

// this code doesn't work as expected
if (random(100) < 20) {
  // Actually a 20% chance
  console.log("Rare Thing 1 (20%)");
} else if (random(100) < 40) {
  // Actually a 32% chance
  console.log("Rare Thing 2 (20%)");
} else {
  // Actually a 48% chance
  console.log("Common Thing (60%)");
}

Pseudorandom vs. Random

Computers are deterministic systems. When a computer is in a particular state and performs a specific instruction, the resulting state should always be the same. The results are never random.

So how can random() produce a random value? Technically, it can’t and it doesn’t. It produces values that appear to be random, called pseudorandom values. Pseudorandom values appear random but are created by a deterministic process.

A common method to create pseudorandom values is a Linear Congruential Generator. LCGs begin with an initial value called the seed, then use multiplication, addition, and modulus (remainder after division) to derive a new, seemingly random value. It is important to understand that the sequence of random() numbers is perfectly predictable if you know the seed.

Toy Linear Congruential Generator

Below is a very basic implementation of an LCG, using small numbers that are easier to reason about. This code follows the same algorithm as the pencil + paper activity above.

Setting the Random Seed

p5 provides randomSeed() to set the seed used by random(). Once you have set the seed, the sequence of values produced by random will always be the same.

The following code example sets the random seed to 12 and then generates 3 random numbers. The results are predictable, and the expected values are shown in the comments. If you change the seed to any other value, you’ll get a different series.

If you set a seed you can use random values in your code but get the same results each time you run your program. This can be a useful feature in some programs and can help with debugging problems. For example, Minecraft creates its worlds procedurally. You can provide a seed for the algorithm to use when making random decisions. If you start two games with the same seed, you’ll get the same world both times.

Be careful when using a seed with random() to get a repeatable sequence. There are at least two common ways for things to get messed up.

• First, if you change your program and add or remove a call to random(), you will alter the position in the sequence for the following calls.

• Second, if your program accepts user input, and that input can influence how many times random() is called, your program can also get off sequence.

Study Examples

The following study examples demonstrate different ways to bias and map random values to get different looks and effects. Carefully study each example to understand how it works. Several of the examples offer varied approaches which can be commented in and out to compare their results.

Skyline

This is the code used to generate the abstract skyline images from the Skyline activity above. The height of each building is determined by the pickHeight() function.

Circle Grid

This example draws a grid of randomly-sized circles. Try commenting in the different methods for choosing the size of each circle. Each method has a distinct look.

Grass

This example draws a row of lines. The height and lean of each line is chosen at random to create a natural, grass-like appearance.

Brownian Motion

This example simulates Brownian motion, which describes the random paths of particles in a liquid or gas. Brownian motion is a common theme in creative coding.

Horizon

This example draws a simple landscape using geometric shapes. It defines functions that draw trees, bushes, and houses, and uses random() to decide what to draw in each position.

Project Case Study: Conspiracy Board

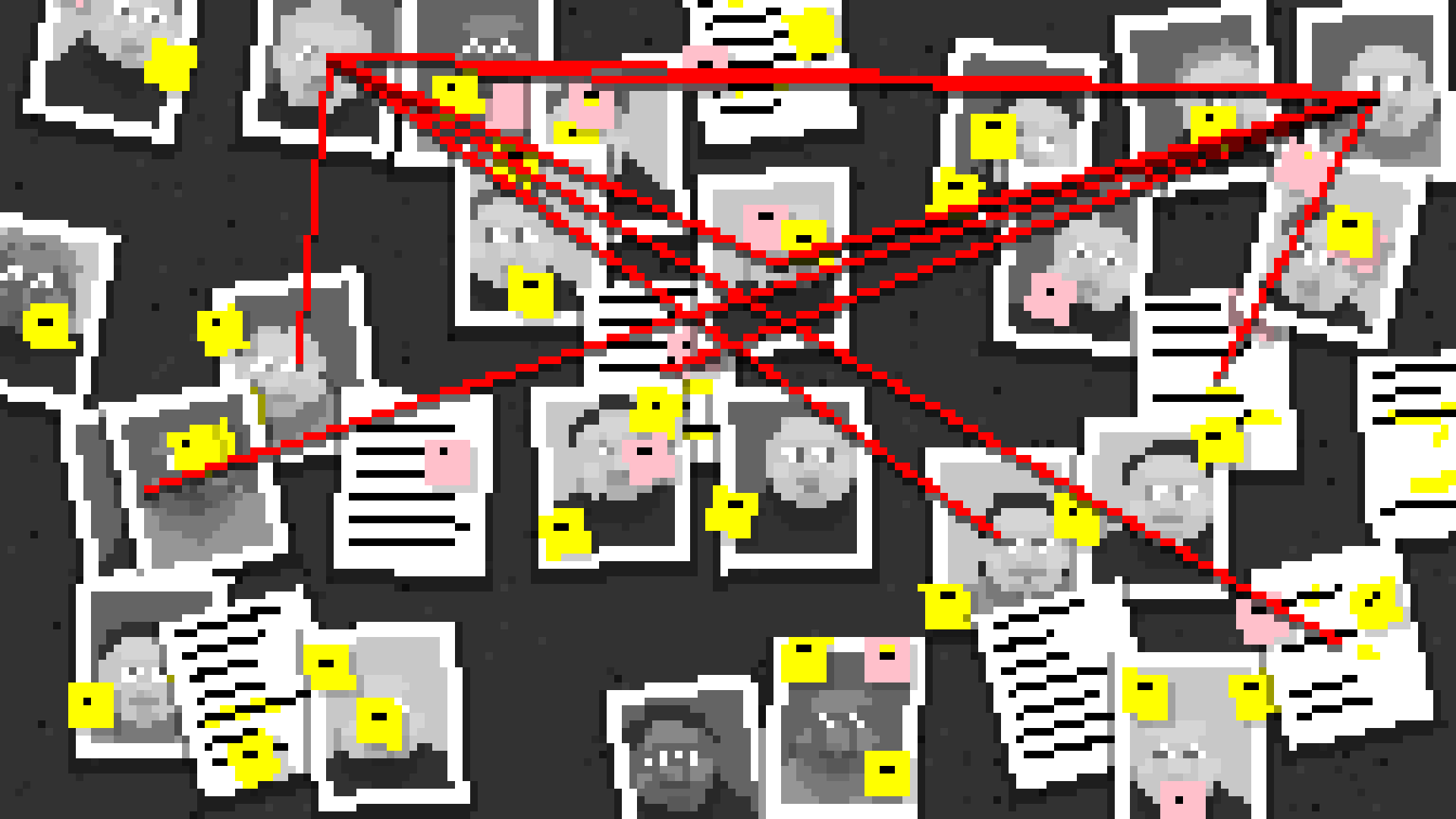
Conspiracy Board is a program that generates pixel-art-style collages of documents, portraits, and strings. It is written in JavaScript using the p5.js library. Visit the case study to learn how it works.

Explore